Morningside Center of Mathematics
Chinese Academy of Sciences
Morningside Center of Mathematics
Chinese Academy of Sciences
华罗庚青年数学论坛
Workshop on Algebraic Geometry
25 June - 29 June, 2018
Lecture series given by 
Takuro Abe (Kyushu University)
Qifeng Li (KIAS)
Wenhao Ou(UCLA)
Botong Wang (Wisconsin-Madison)
Junyi Xie (CNRS, France)
Invited talks given by
Yewon Jeong (KIAS)
Duo Li (Tsinghua University)
Bong Lian (Brandais University)
Pedro Montero (AMSS)
Shigeru Mukai (RIMS)
Qizheng Yin (Peking University)
Organizer:
Baohua Fu (MCM & AMSS)
Shigeru Mukai(RIMS)
Xiaotao Sun (Tianjin University)
Supported by 
Academy of Mathematics and Systems Science, CAS
Morningside Center of Mathematics, CAS
Schedule:
|
|
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
|
9:30—10:30 |
WANG |
ABE |
XIE |
Y. Jeong |
B. Lian |
|
10:45-11:45 |
OU |
XIE |
LI |
Q. Yin |
P. Montero |
|
2:00—3:00 |
XIE |
LI |
ABE |
Free |
D. Li |
|
3:15—4:15 |
LI |
OU |
WANG |
15:30—16:30 S. Mukai |
|
|
4:30—5:30 |
WANG |
ABE |
OU |
Minicourses:
Free arrangements of hyperplanes and applications
Takuro Abe(阿部拓郎)
An arrangement of hyperplanes is a finite set of linear hyperplanes in a vector space. To an arrangement, we may associate the module of logarithmic derivation modules, which is reflexive but not free in general. So we say that an arrangement is free if it is a free module. The logarithmic derivation module of arrangements was first studied by K. Saito when the arrangement is the set of reflecting hyperplanes of all reflections of Coxeter groups. In this case the arrangements are all free, and we can construct the basis in terms of the invariant theory. Since there are a lot of intersections between algebra, geometry and combinatorics in this case, the freeness for a general arrangement has been intensively studied by several mathematicians like K. Saito, L. Solomon, P. Orlik, and H. Terao.
We start explaining the basic properties of free arrangements, and introduce recent developments based on the splitting theory of vector bundles over the projective spaces. If time permits, we introduce an interesting relation between the logarithmic derivation module and the cohomology group of the regular nilpotent Hessenberg varieties.
Recognizing rational homogeneous spaces of Picard number one by its varieties of minimal rational tangents
Qifeng Li (李起峰)
In the series work on deformation rigidity of rational homogeneous spaces of Picard number one, Hwang and Mok develop the theory of varieties of minimal rational tangents (VMRT). The theory of VMRT is a powerful tool to study Fano manifolds of Picard number one. The basic idea is that a large part of the global geometry of a Fano manifold of Picard number can be controlled by its VMRT at a general point. The equivalence of VMRT structure is one of the main problems in this theory. When the VMRT structure is modeled on some well-known manifolds such as G/P_max, the equivalence problem is the question whether we can recognize the manifold by its VMRT’s.
In this lecture series, we will start from basic notions in VMRT theory, and introduce the problem of equivalence of VMRT structures. We will also have a short review on its applications to such as deformation rigidity, classification problems and contact geometry. Then we will give an overview of historical solution of recognizing G/P_max by its VMRT’s. Finally, we will give an introduction to the part of Cartan geometry that is closely related to VMRT theory. This is at present the main machinery for recognizing a (quasi)homogeneous manifold from its VMRT’s.
Bimeromorphic Geometry of K ?hler Threefolds
Wenhao Ou (欧文浩)
In this series, we will describe bimeromorphic geometry of K?hler threefolds, which is an analogue of birational geometry of projective varieties. The main goal is to generalize Minimal Model Programs (MMP) in the setting of K?hler geometry. The essential theorem in classic MMP is Mori's bend-and-break theorem, which enables us to find rational curves in a projective variety. The proof of this theorem relies on the pure algebraic method, ``reduction modulo p ''. For a K?hler variety however, it is sometimes even difficult to find subvarieties.
A breakthrough in this direction has been made by H?ring and Peternell. They established MMP for non uniruled K?hler threefolds (that is, K?hler threefolds which are not covered by rational curves), and hence proved the existence of minimal models. They also built certain special MMP for uniruled K?hler threefolds, and conclude the existence of Mori fiber spaces. Together with Campana, they proved the abundance theorem for K?hler threefolds as well. Motivated by their ideas, in a recent joint work with Das, we show the log abundance theorem for K?hler threefolds.
The first talk of the series will be introductory. We will start by going through classifications of compact complex curves and surfaces. Then we will review some main theorems in classic MMP, and introduce their conjectural analogues in K?hler geometry. The remaining two talks will focus on the techniques used in the constructions of MMP for K?hler threefolds, and in the proofs of abundance theorems.
Algebraic dynamics of polynomial endomorphisms of the affine plane
Junyi Xie (谢俊逸)
In these lectures, we study the algebraic dynamics of polynomial endomorphisms of the affine plane. In particular, we introduce the valuation tree at infinity and use it to study the periodic points and periodic curves.
Kazhdan-Lusztig theory of matroids
Botong Wang (王博潼)
Matroids are combinatorial generalizations of configuration of points in vector spaces, or equivalently, hyperplane arrangements. I will discuss two conjectures in matroid theory. The first is a “top-heavy” conjecture by Dowling and Wilson in the 70’s, and the second is some non-negativity conjecture about the Kazhdan-Lusztig polynomial of matroids introduced recently by Elias-Proudfoot-Wakefield. I will explain the proofs of the conjectures in the realizable case (the first conjecture by Huh and myself, and the second by E-P-W). The proof uses Hodge theory of the matroid analogous of the Schubert varieties. I will also talk about some work in progress of extending the proof to the non-realizable case, which is joint with Tom Braden, June Huh, Jacob Matherne and Nick Proudfoot.
The second talk is an introduction to matroids. I will talk about the definition and basic properties of matroids, and how they arise naturally from graphs and vector configurations.
The third talk is on Hodge theory of matroids. I will introduce the Chow rings of matroids, and the work of Adiprasito-Huh-Katz on the Hodge theory of these Chow rings. I will also discuss some log-concavity results as applications.
Invited talks:
Moduli of second fundamental forms of a nonsingular intersection of two quadrics
Yewon Jeong
In 1979, Griffiths and Harris raised a question on the moduli of second fundamental forms of a projective complex submanifold of codimension two. We will report on our study of the question for complete intersections of two quadrics.
On projective varieties with strictly nef tangent bundles
Duo Li(李铎)
In this talk, we study smooth complex projective varieties X such that some exterior power of the tangent bundle is strictly nef. We prove that such varieties are rationally connected. We also classify the following two cases. If the tangent bundle is strictly nef, then X isomorphic to the projective space. If the second exterior power of TX is strictly nef and if X has dimension at least 3, then X is either isomorphic to projective space or a hyperquadric. This is a joint work with Wenhao Ou and Xiaokui Yang.
Some recent applications of the Riemann-Hilbert problem for period integrals
Bong Lian (连文豪)
This will be a brief introduction to the Riemann-Hilbert problem for period integrals, followed by a discussion of one or two recent applications. The first concerns with the null variety of a class of generalized hypergeometric functions, which are higher dimensional analogues of problems studied by Stieltjes, Hilbert, Klein, Hurwitz and others who considered zeros of the Gauss hypergeometric function _2F_1(a,b,c;z)$. The second application is on the recent proof of one important case of the hyperplane conjecture in mirror symmetry. This is joint work with J. Chen, A. Huang, S.-T. Yau and M. Zhu.
A characterization of some Fano fourfolds through conic fibrations
Pedro Montero
Let X be a Fano manifold of dimension n. A conic bundle on X is a fiber type contraction with fibers of dimension one. In this talk, we will highlight the relation between the relative Picard number of conic bundles on X and the so called "Lefschetz defect", introduced by Casagrande and related with the Picard number of divisors on X. After giving a general account of the known results, we will address the first unknown case: Fano fourfolds with Lefschetz defect 3. In this case we get general results on the structure of these varieties (bounds on the Picard number of X, rationality and classification of the varieties arising as targets of conic bundles) and some results towards the classification of such fourfolds. This is a joint work with Eleonora Romano (University of Warsaw).
Rational curves and special subvarieties in holomorphic symplectic varieties
Qizheng Yin (訚琪峥)
We discuss the search of special subvarieties inside holomorphic symplectic (a.k.a. hyper-K?hler) varieties, with emphasis on an approach via rational curves. This is motivated by the Beauville-Voisin study of algebraic cycles on holomorphic symplectic varieties. Many open questions will be presented. We also give concrete examples/counterexamples in the case of the Fano variety of lines in a cubic 4-fold. Joint work with Georg Oberdieck and Junliang Shen.
Colloquium:
Playing with plane cubics, rational sextics and Cremona transformations
15:30—16:30 on Friday
Shigeru Mukai (向井茂)
Several theorems, such as Pappus’, Miquel’s and Desargues’ in elementary geometry are theorems of projective geometry also. Moreover, they have infinite symmetries of Cremona transformations of the projective plane. After explaining it for pencil of cubics, I will move to rational sextics and present an example with action of a non-commutative free group consisting of infinte Cremona transformations.
Arrival Information:
Transportation
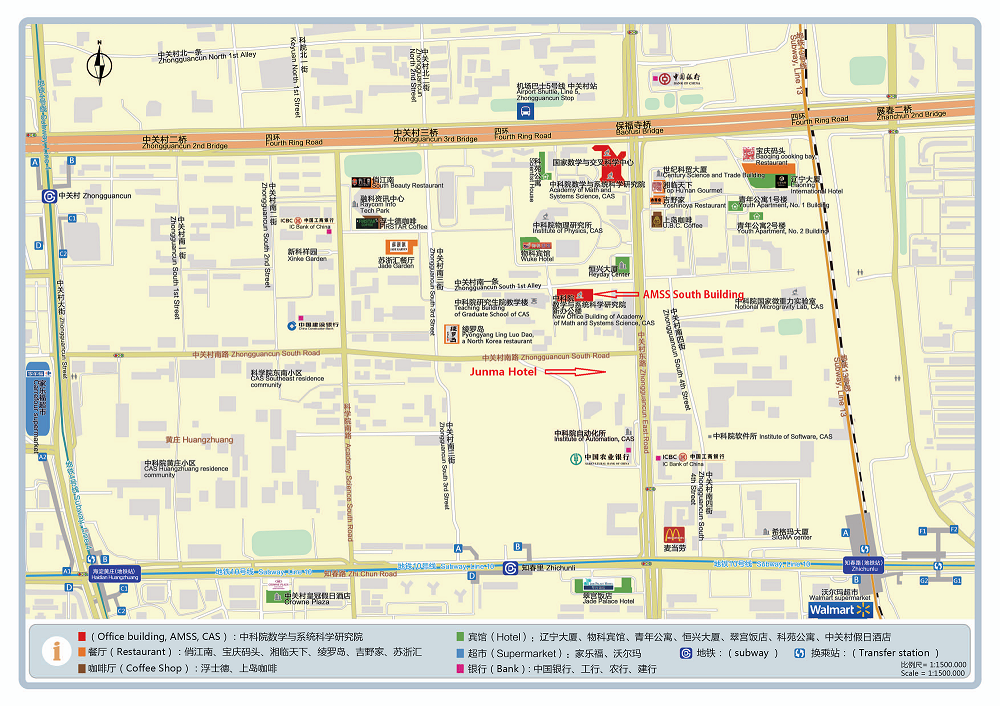
You can take the following 3 vehicles and then go to hotel or conference buidling by walk accoring to the local maps below.
· Airport Shuttle
Taking airport shuttle line 5 to Zhongguancun (中关村) Station (the last station) which costs about 30 Yuan.
http://en.bcia.com.cn/traffic/airbus/index.shtml
· Subway
Taking subway line 10 to Zhichunlu (知春路) or Zhichunli (知春里) Station which costs about 30 Yuan from airport or 5 Yuan from train station.
· Taxi
Taking taxi to Baofusiqiao (保福寺桥) which costs about 100 Yuan from airport or 50 Yuan from train station. You can print the following message and show it to taxi driver.
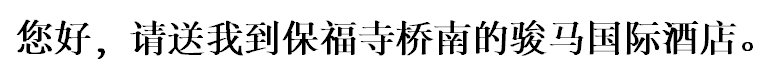
Hotel
All speakers will stay in Junma International Hotel. http://www.junmahotel.com/
Local Maps:
| 相关附件 |
|---|
| 相关文档 |
|---|
中国科学院晨兴数学中心2014-2019版权所有 京ICP备05002806号
北京市海淀区中关村东路55号 邮政编码:100190
电话:86-10-82541165 Email: mcmadmin@math.ac.cn